Volume Rendering of Neural Implicit Surfaces

Abstract

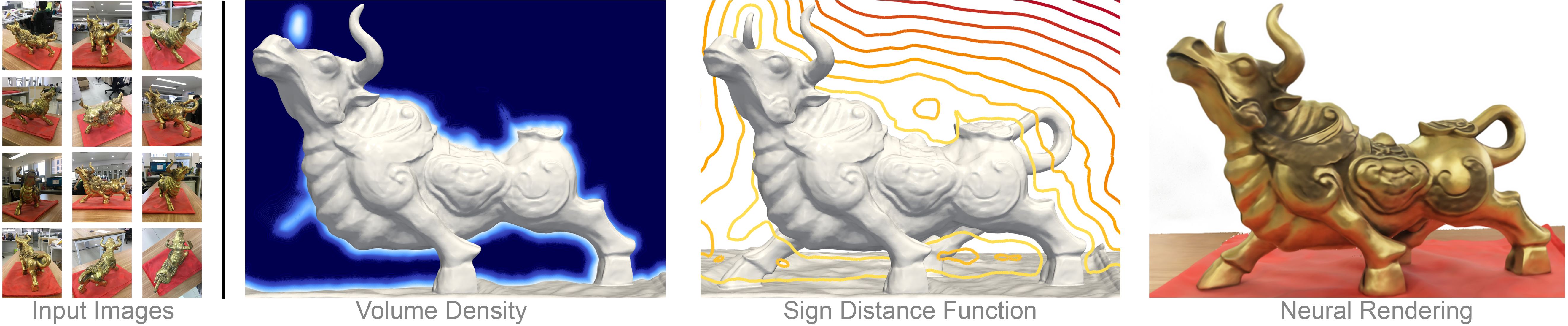
Neural volume rendering became increasingly popular recently due to its success in synthesizing novel views of a scene from a sparse set of input images. So far, the geometry learned by neural volume rendering techniques was modeled using a generic density function. Furthermore, the geometry itself was extracted using an arbitrary level set of the density function leading to a noisy, often low fidelity reconstruction. The goal of this paper is to improve geometry representation and reconstruction in neural volume rendering. We achieve that by modeling the volume density as a function of the geometry. This is in contrast to previous work modeling the geometry as a function of the volume density. In more detail, we define the volume density function as Laplace’s cumulative distribution function (CDF) applied to a signed distance function (SDF) representation. This simple density representation has three benefits: (i) it provides a useful inductive bias to the geometry learned in the neural volume rendering process; (ii) it facilitates a bound on the opacity approximation error, leading to an accurate sampling of the viewing ray. Accurate sampling is important to provide a precise coupling of geometry and radiance; and (iii) it allows efficient unsupervised disentanglement of shape and appearance in volume rendering. Applying this new density representation to challenging scene multiview datasets produced high quality geometry reconstructions, outperforming relevant baselines. Furthermore, switching shape and appearance between scenes is possible due to the disentanglement of the two.

Method

We propose VolSDF: a novel parameterization for the density in neural volume rendering. We suggest to model the density using a transformed learnable Signed Distance Function (SDF) , namely:

where are learnable parameters, and is the Cumulative Distribution Function (CDF) of the Laplace distribution with zero mean and scale.
This seemingly simple definition provides a useful geometric inductive bias, and it allows bounding the approximation error of the opacity and consequently devise a sampling algorithm for approximating the volume rendering integral.

Sampling algorithm

Here we illustrate our iterative sampling algorithm for a single ray indicated by the white pixel, and we show the current approximated opacity, and the samples that were produced from it and used for the rendering approximation. For the same ray we also show the true opacity error, and error bound.

Multiview 3D Reconstructions

Examples of reconstructed 3D geometry and rendering of novel views from the two multiview datasets DTU and BlendedMVS.

DTU dataset

BlendedMVS dataset

Disentangling geometry and appearance

Examples of the unsupervised disentanglement of geometry and radiance field. The diagonal depicts the independently trained scenes, while the off-diagonal demonstrates post-training mix and match of geometries and radiance fields.